INSIDE
RACING

 T E C H N O L O G Y

 
  
IRT Home

News Page

Contents Page

Newsletter & Books

email Paul

This excerpt from The Racing & High-Performance Tire appeared in the February 2004 issue of Sports Car magazine.

Chapter 6: Tire Behavior

After chapters on rubber, friction, and tire design and manufacture, here's what we know so far:

A tire, one of the most useful and complicated devices made, is a gas-pressurized, textile/rubber composite with a rubber traction coating. Rubber is a mixture of polymers, reinforcing fillers, and other chemicals that, after vulcanization, have viscoelastic characteristics that are not fully understood. Tires are difficult to manufacture consistently, but current technology and manufacturing facilities produce an extremely reliable, durable, and inexpensive product. A finished tire is a bonded unit, so failed tires are difficult to analyze post-failure. Rubber friction, mainly due to adhesion and deformation, exhibits viscoelastic effects and is sensitive to compounding variations, vertical loading, sliding speed, and temperature.

Now let's look at some of the details of how tires behave during use.

How a Car Turns a Corner: Revisited

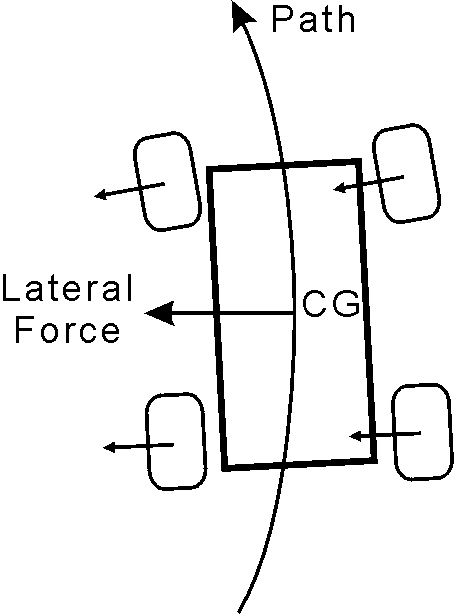
Fig. 6.1

At any moment in time a car turning a corner is accelerating toward the center of an instantaneous circular arc as in Fig. 6.1. The radius of that arc might be changing, but at any instant the path is a specific arc. The car's tires supply the force to turn the car. That force is called lateral force or side force or just grip. In this schematic we combine the lateral forces of the four tires and have it acting on the center of gravity (CG) of the car.

Slip Angle

A tire produces lateral force with a slip angle, shown in Fig. 6.2. Slip angle happens when the steering wheel is turned from straight ahead and it's the angle, "a" in the schematic, between where the tire is pointed and where the car is actually going.

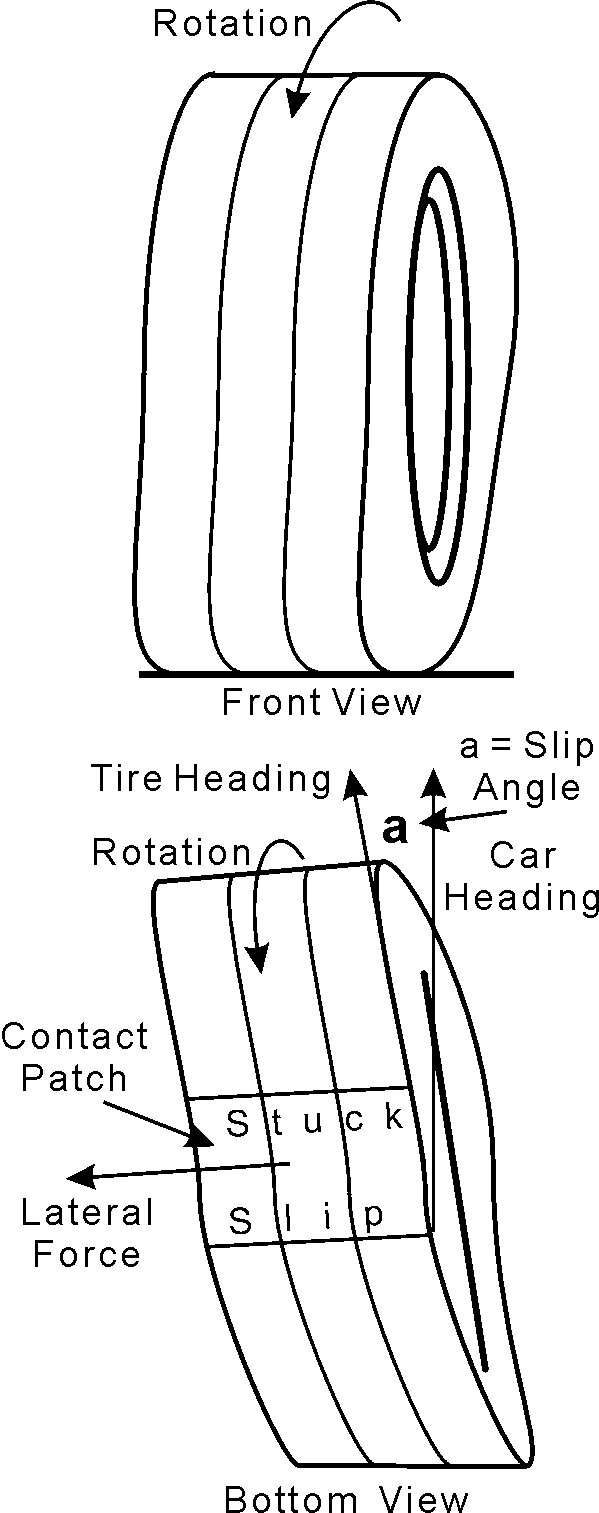
Fig. 6.2

The elastic nature of a tire makes a slip angle possible. The tire grips the road but also yields to external force, resists movement with an opposing force, and recovers when the external force is removed. This elastic characteristic of a tire allows the tire to be pointed in a direction different from the direction the car is headed.

It's important that we understand what's going on in the contact patch between road and tire that creates a slip angle. The tire is rolling, so any one point on the tread rotates into and out of the contact patch with every revolution. When the tire is rolling in a straight line that point on the tread sees a regularly repeating thump of vertical force as it rotates into the contact patch and momentarily bears this tire's share of the vehicle weight.

As soon as the driver turns the steering wheel, conditions change at the contact patch. Steering input causes the tire to turn, and now the leading edge of the tread rotates on to the road slightly to one side of the rest of the contact patch. As the tire rolls, each small increment of tread rubber coming onto the road sits down another small distance toward the direction the tire is pointed.

As the car's weight comes onto these small increments, they stick to the road. The tread is now pulling the rest of the tire and generating forces that go through the wheel and the suspension to turn the car. The force needed to change the car's path is generated by the tire. This is called lateral force or side force.

As in Chapter 1, we can use the analogy shown in Fig. 6.3 of a person walking to further explain slip angle. A person walking on a circular path changes direction in small increments. At each step a foot is turned in a small angle toward the path of the arc. The heel contacts the ground and the rest of the shoe comes down in this new direction. As weight comes onto the shoe sole, the shoe is pointed in the new direction. The next step also changes the walker's path a small amount. These small changes continue to build up and the direction the walker is headed changes also.

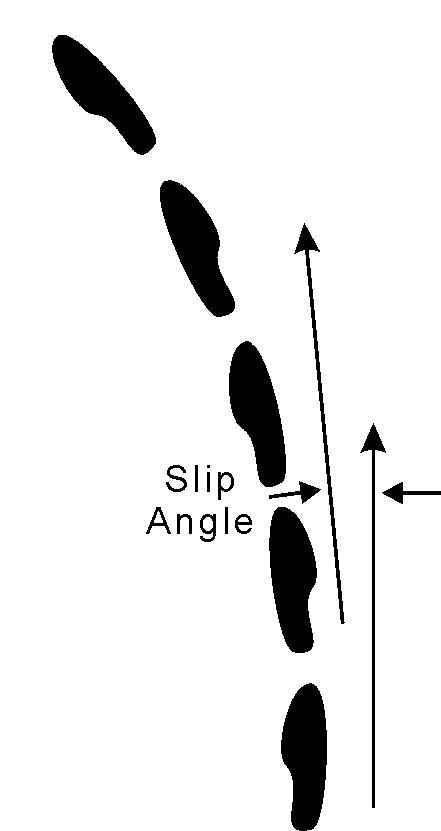
Fig. 6.3

That's exactly what happens when a tire is given some steering input. Each small increment of tread rubber rotating into contact with the road surface latches onto the road surface a small increment toward a new heading. As long as the steering input remains the same, each increment of the tread contacts the road the same amount toward the new direction. The rest of the contact patch thinks it's headed in the old direction, but the old contact patch continually rotates out of road contact. The next time that part of the tire touches down, the heading of the tire and car will have changed.

The tire tread actually deforms as it rotates through the contact patch area and then recovers as the car's weight comes off the contact patch. The force needed to deform the tire is what produces the lateral force needed to change the path of the car.

When the front tires respond to steering input with a slip angle and begin to develop lateral forces, the front of the car turns to a new heading and the entire car rotates in yaw. If the rear wheels were mounted like casters they would swivel and the rear of the car would spin outward, away from the turn. But the rear tires are fixed in direction and they resist yawing with their own slip angles and lateral forces.

Lateral Force vs. Slip Angle

Fig. 6.4 shows the general relationship between the lateral force a tire generates and the slip angle of the tire. A tire does not generate side force until it is steered away from its current course and it assumes a slip angle. The shape of this curve is not the same for all tires. A graph like this is a specific characteristic of a tire design-the result of the cord angles and rubbers used in the tire structure and the rubber compounds in the tire tread.

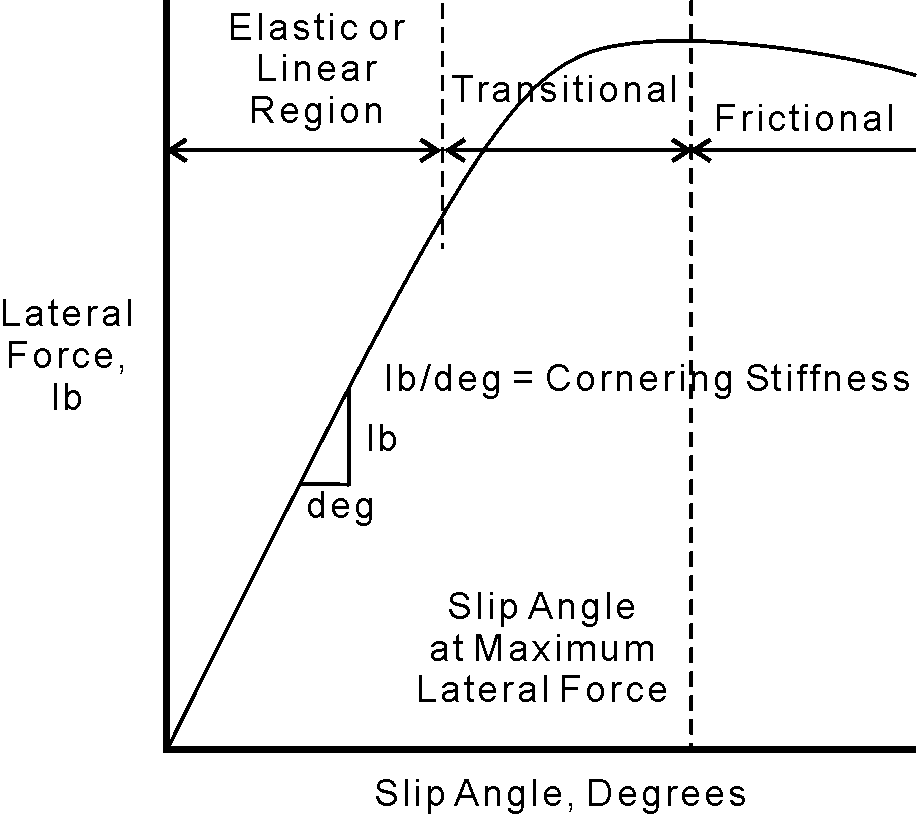
Fig. 6.4

Notice that this curve has three distinct shapes. First there's an almost straight section at small slip angles where an increase in slip angle gives a proportional increase in lateral force. The slope of this section of the curve is the "stiffness" of the tire. In this region of the curve the tread is not sliding on the road at any point in its contact patch. A tire designed to have more stiffness in the tread and sidewalls will have a steeper slope in this area of the curve.

At higher slip angles portions of the tire patch are sliding, and you get less increase in lateral force with an increase of slip angle. This is called the transition region. As the curve tops out, more of the contact patch is sliding and the tire produces less lateral force. After the peak of the curve, lateral force can fall off 30% within a few degrees of extra slip angle. At these high slip angles most of the contact patch is sliding, producing a lot of heat and wear.

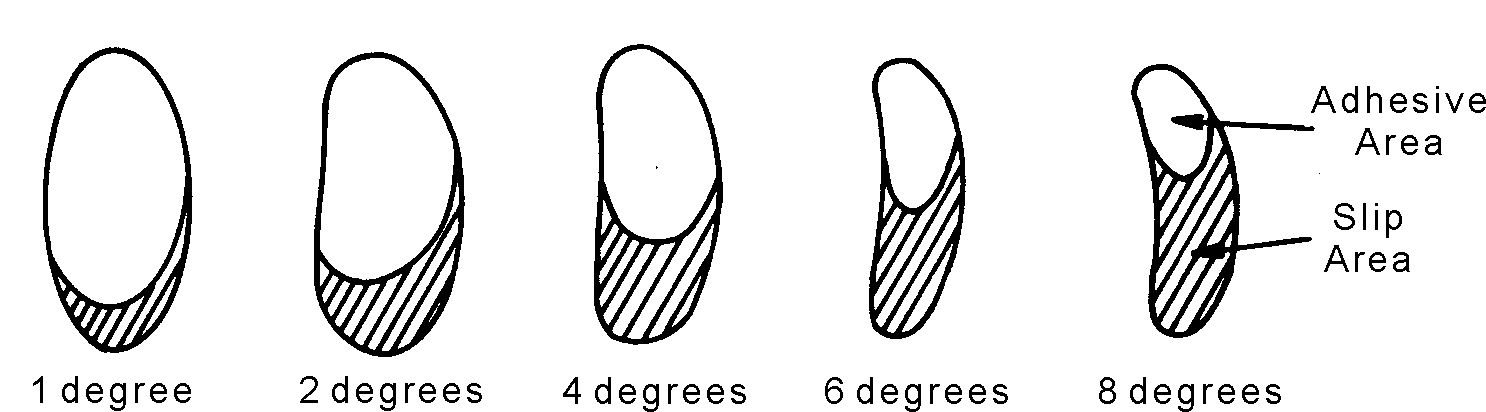
Figure 6.5

The schematics in Fig. 6.5 came from visual observation of contact patch shapes at varying slip angles. The tire is rolling in the direction of the top of the page and is turning left. This contact patch is much more narrow than that of a current tire, but that helps us see the changes more easily. Notice how the leading edge of the contact patch curves toward the turn. This is the result of slip angle; the tire is pointed in the direction forced by steering input. The leading edge of the contact patch is pointing in the steering direction while the rearward portion of the contact patch lags behind on the old heading.

Longitudinal Forces

The forces on a tire during acceleration and braking deform the sidewall enough that the contact patch moves a noticeable amount. The three schematics in Fig. 6.6 show how braking and driving forces can move the contact patch compared to static conditions.

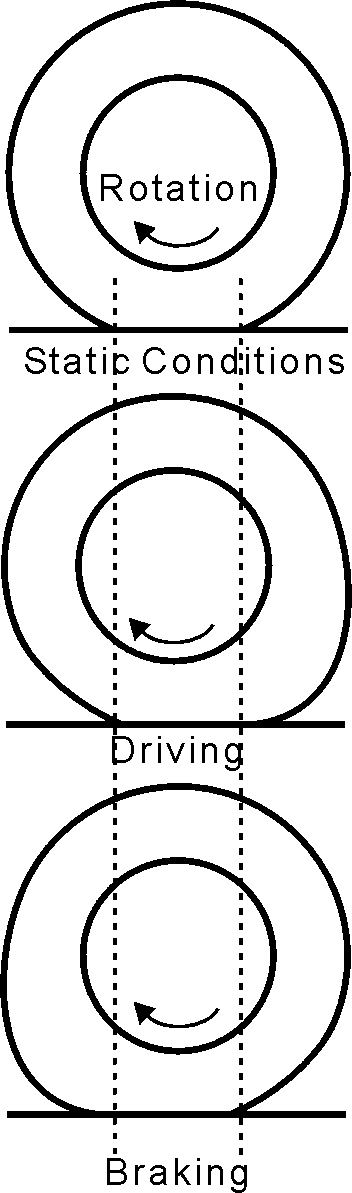
Fig. 6.6

During braking and acceleration tires generate longitudinal force, and there is some longitudinal slip between the tread and the road. This shows up as a difference between the actual rotation of the tire and the rotation needed if there were no slip. Under hard acceleration the tire turns a little faster, and during hard braking the tire rotates less than it would if there were no slip. These two graphs show driving (Fig. 6.7) and braking forces (Fig. 6.8) vs. percent slip.

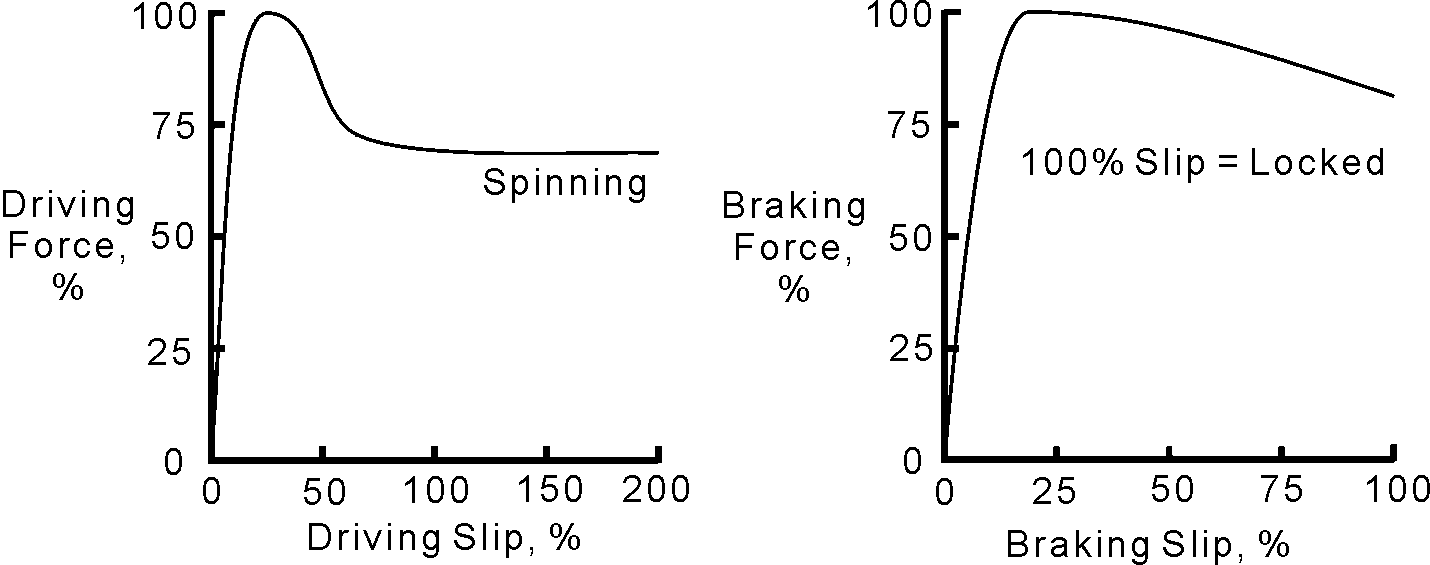
Fig. 6.7 Fig. 6.8

The shape of these two curves suggest the tire reacts to braking and driving forces in different ways. As soon as driving slip approaches 50%, driving force falls off rapidly. Braking slip falls off at only 25% slip, but the force reduction is more gradual. I don't know the source of the data for these graphs but they might look more alike if the percent-slip scale were the same.

Another possibility is that the driving-force curve drops off and flattens out because the tire is still spinning and the tread surface has a chance to cool, where the braking tire is locked at 100% slip and slides on the same contact patch. This heats up the rubber, lowering its friction capability. I'll bet the braking curve continues to fall off after 100% slip, off the scale of this graph.

Of course these curves represent generic data from passenger-car tires. Testing at high slip is difficult due to the forces involved. Probably the only valid test vehicle for racetires is a competitive, fully-instrumented racecar driven by a world-class driver. Even then the tire/road/driver system varies continuously creating noise in the data.

Combined Forces

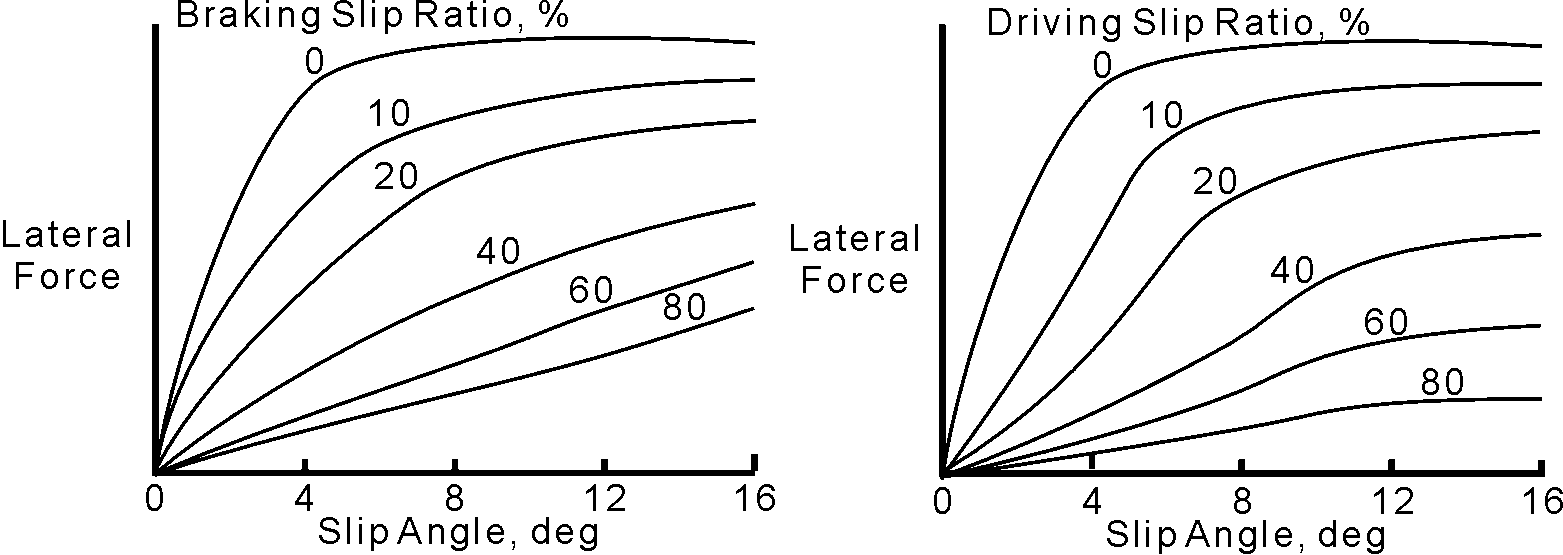
Fig. 6.9 Fig. 6.10

Data showing tire behavior under a combination of both lateral and longitudinal slip is almost nonexistent outside of the tire companies' test facilities. Graphs similar to Fig. 6.9 and 6.10 appear in various books and are very general. The main point made is that lateral force falls off rapidly with any additional slip due to acceleration or braking.

Friction Circle

The graphs above show that tires produce maximum lateral force when there are no driving or braking forces. The friction circle graphic in Fig. 6.11, actually a half-circle because the other half would look roughly the same, illustrates how lateral force falls off in the presence of braking or acceleration. The concept is equally applicable to a single tire or a vehicle.

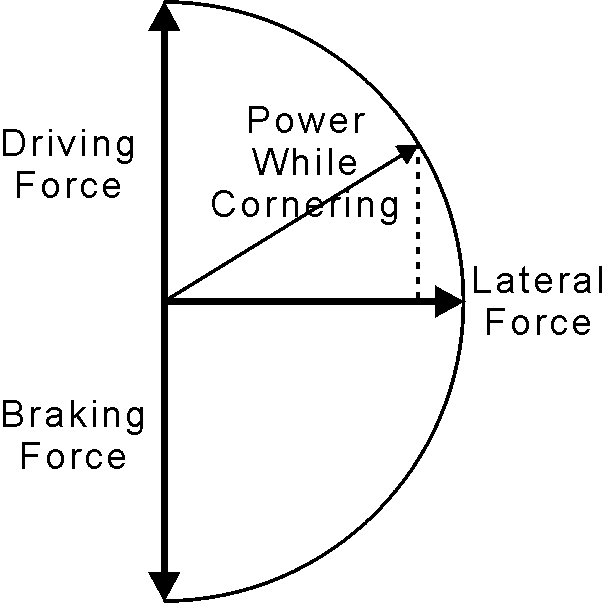
Fig. 6.11

The three thick arrows show maximum driving, braking, and lateral forces when those are the only forces present. When the tire sees a combination of forces, driving force and lateral force are shown here, maximum lateral force is not available. In this example, adding driving power to the tire reduces the available lateral force. Of course this is what we feel powering out of a slow corner-power oversteer-one of the most fun things you can do with a car.

Lateral Deformation of the Tread

It bears repeating that it is the elastic characteristic of the pneumatic tire that allows the generation of a slip angle, and it is the forces resisting the deformation of the tire structure combined with the tread's grip on the road that allows a car to turn a corner at speed. The schematic in Fig. 6.12 represents tread deformation in the contact patch of a tire rolling to the left with some right-hand steering angle and a resulting slip angle. The dotted line with an arrowhead represents the direction the vehicle is headed. The angle between the vehicle heading and the wheel heading is the slip angle.

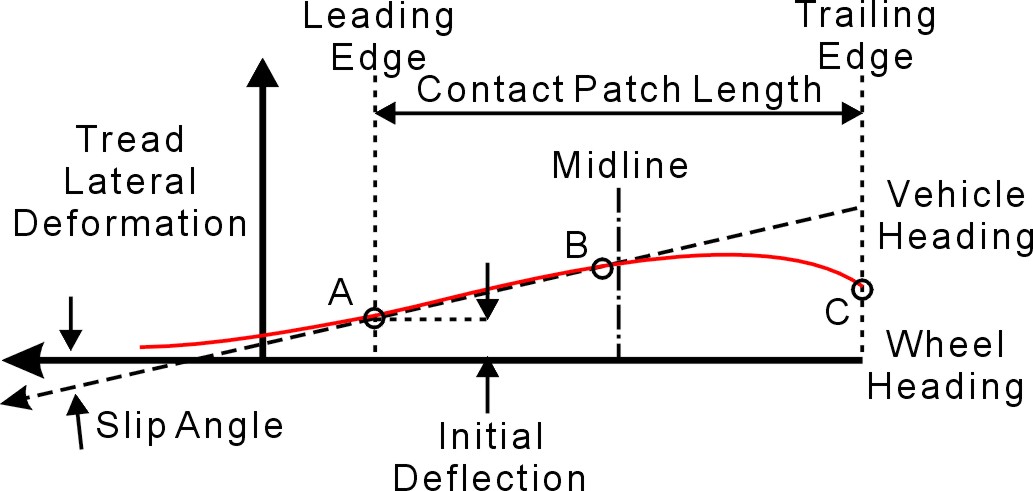
Fig. 6.12

The curved solid red line represents tire lateral deformation from its unstressed position. Once again, it is the tire's resistance to this deflection that creates the lateral force that turns the car. The curved line tracks the lateral deformation of a single point on the surface of the tread rubber as it travels through the contact patch and is deformed by the road acting on the tire. The solid line with a left-pointing arrow is the zero-deflection line. The difference between those two lines is the distance the tire deflects.

The tread rotates into the contact patch at point A, and the lateral deflection at point A is called the initial deflection. Point A marks the leading edge of the contact patch, but deflection starts prior to that. The tire carcass has some stiffness and the tread is even more stiff, so there has to be some deflection starting well before the tire rotates into the contact patch.

From point A to point B, somewhere near the midline of the contact patch, the tread stays stuck to the road (at this slip angle anyway) and lateral deflection in the carcass and in the tread rubber increases linearly. But at some point the force required to deflect the tread exceeds the local friction coefficient times the local load, and the tread begins to slide on the road. At higher slip angles sliding starts farther forward, as we saw in the drawings in Fig. 6.5.

At point B the tread begins to recover from maximum lateral deflection and at point C the tread rotates out of the contact patch. Notice that there is still some lateral deflection at C. The tire has to rotate farther before the lateral deflection fully recovers. Once again it is the remarkably strong but elastic nature of a tire that enables it to deform, assume a slip angle, and generate turning forces.

In the book I follow up this section with explanations of why wide tires generate more grip and why tires are load sensitive.

A third excerpt will appear in the March issue of Sports Car and later, here.