INSIDE
RACING

 T E C H N O L O G Y

 
  
IRT Home

News Page

Contents Page

Newsletter & Books

email Paul

Rubber Friction

Simple Friction

We need to overcome friction in order to move one material against another, a common phenomenon in our everyday world. Nails hold because of friction. We couldn't walk or even crawl without friction.

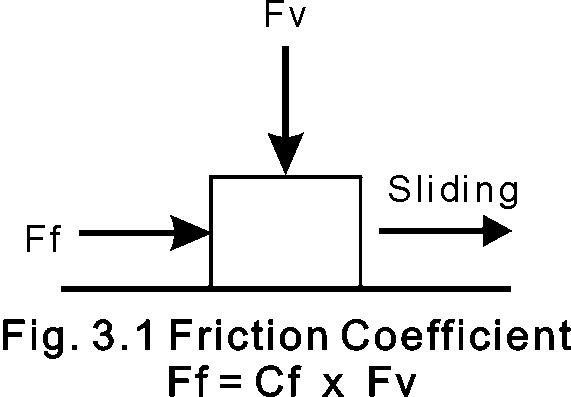
This general equation and Fig. 3.1 describe friction:

Ff = Cf x Fv,

where Friction force (Ff) equals the coefficient of friction (Cf) times the vertical force (Fv).

This equation says the force necessary to move a material at a steady speed on another material is proportional to the force pressing the two materials together and also proportional to a nondimensional constant (Cf) produced by testing the two materials together. The static coefficient of friction is usually larger than the dynamic coefficient of friction for the same material. This means you need a little more force to start a material sliding than you do to keep the material moving at a steady speed.

Table 3-1: Typical Values of Cf for Combinations of Materials

Material	Cf
Wood on wood, dry	O.25 - 0.50
Metal on oak, dry	O.50
Leather on metal, dry	O.56
Metal on metal, dry	0.15 - 0.20
Rubber on glass, dry	2 +

A Cf greater than 1.0 means it takes more force to move a rubber block on glass than the force pressing the block onto the surface. This gives us a clue that with rubber there is more going on than simple friction.

Rubber Friction

Rubber generates friction in three major ways: adhesion, deformation, and wear. Fig. 3.2 describes these three components making up the total friction force experienced by a rubber slider moving across the surface of a road in the direction of speed V.

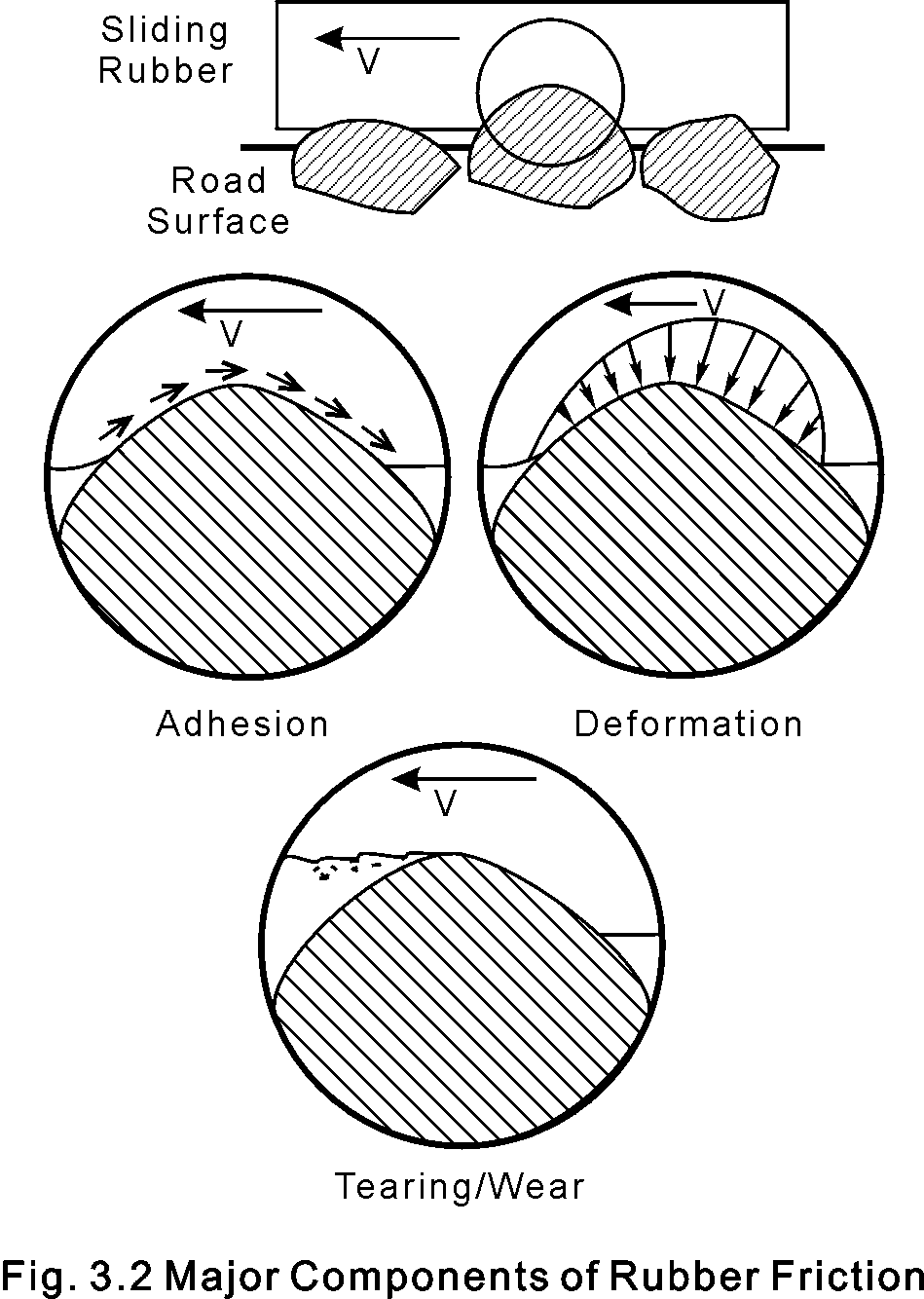
Adhesion

Adhesion is a property of rubber that causes it to stick to other materials, as we see with adhesive tape. Adhesion is generally thought to be the result of momentary molecular bonding between the two surfaces. If bond strength is the same at all the bond sites the force that resists sliding is proportional to the total of all the minute areas of contact. If the two surfaces were perfectly smooth the true area of contact would be the same as the observed area of contact, but this is not the case. Real surfaces are actually very rough on the molecular scale and contact is limited to the highest protuberances on each of the two surfaces. The true area of contact depends on the surface profiles, properties of the materials, and the contact pressure.

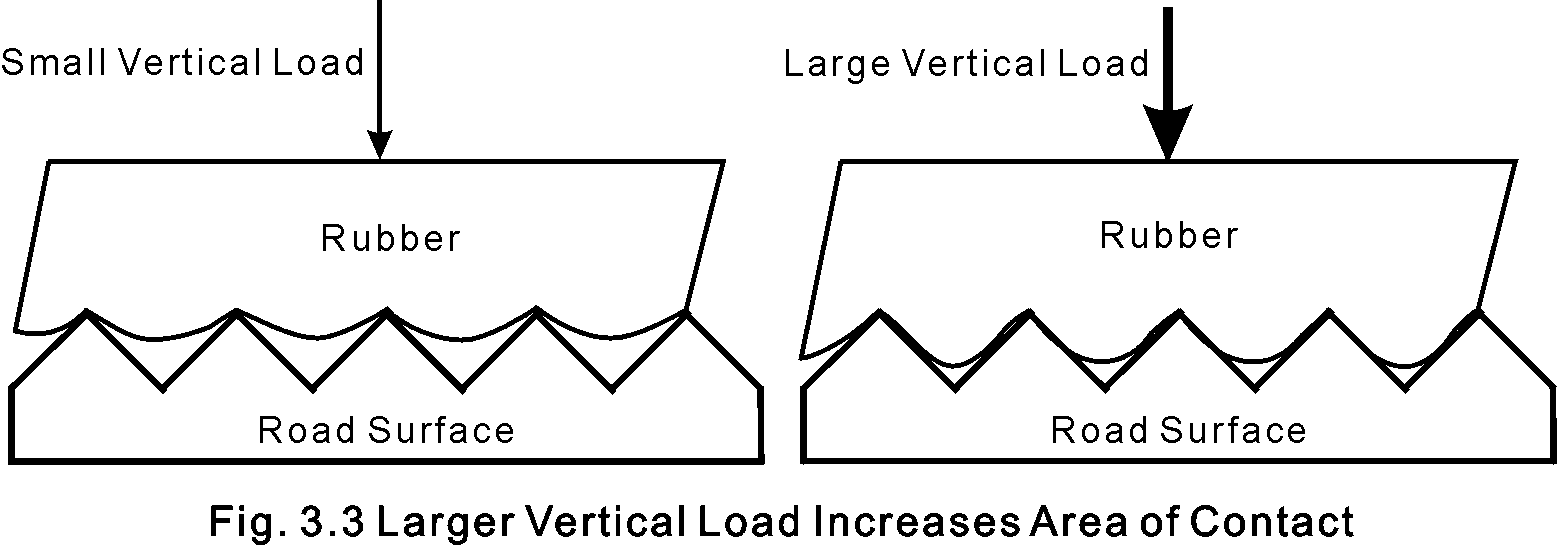
As you can see in Fig. 3.3, larger loads on the rubber presses the road irregularities into the rubber, increasing the contact area. More area in contact means more adhesion between the surfaces and higher friction forces. This situation satisfies the general requirements of the friction equation, Ff = Cf x Fv.

Deformation: Mechanical Keying

Rubber in contact with a smooth surface (glass is often used in testing) generates friction forces mainly by adhesion. When rubber is in contact with a rough surface, another mechanism, deformation, comes into play.
Movement of a rubber slider on a rough surface results in the deformation of the rubber by high points on the surface called irregularities or asperities. A load on the rubber slider causes the asperities to penetrate the rubber and the rubber drapes over the asperities. The energy needed to move the asperities in the rubber comes from the differential pressure across the asperities as shown in Fig. 3.4, where a rubber slider moves on an irregular surface at speed V.

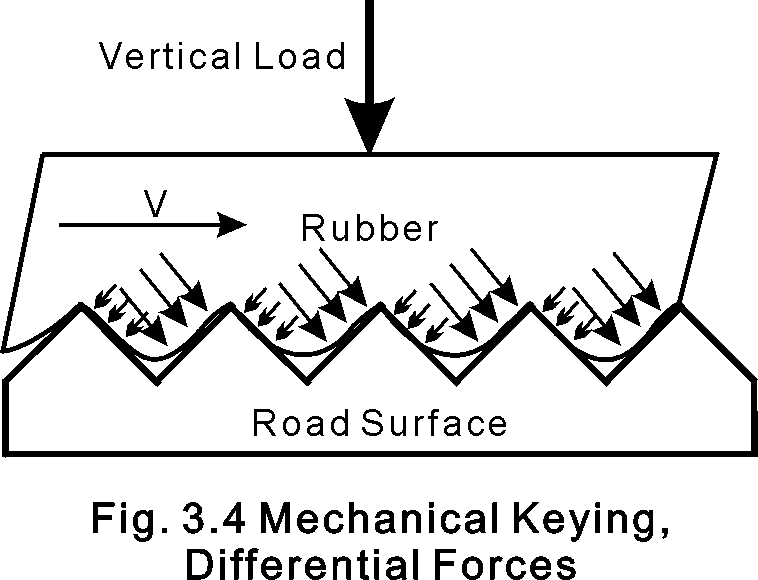
A wet surface prevents contact between the rubber and the surface, blocking the formation of adhesive forces. Friction forces due to deformation, also called mechanical keying, provide most of the friction force between a tire and a wet surface.

Tearing and Wear

In addition to adhesive friction and deformation friction, rubber produces traction forces by means of tearing and wear. As deformation forces and sliding speeds go up, local stress can exceed the tensile strength of the rubber, especially at an increase in local stress near the point of a sharp irregularity. High local stress can deform the internal structure of the rubber past the point of elastic recovery. When polymer bonds and crosslinks are stressed to failure the material can't recover completely, and this can cause tearing. Tearing absorbs energy, resulting in additional friction forces in the contact surface.

Wear is the ultimate result of tearing. When local stresses increase in strength past initial tearing or remain at high strength for a period of time, that tearing can result in separation of material. The tire debris, bits of rolled-up rubber, you see on a racetrack is the result of rubber being torn and abraded from the tire. When these pieces separate from the tire, especially a race tire, they can be hot enough to stick together, so clumps of rubber as large as a baseball can be found on a racetrack or stuck to a racecar. In a later chapter we'll look closer at worn tires and what they can tell us.

Total Friction

Now we can write a more general equation for rubber friction:

Ftotal = Fad(hesive) + Fdef(formation) + Fwear

The naming of these components is strictly arbitrary. There are probably other friction components if you look in more detail, but we'll refer to them by these names in this discussion. Let's look in more detail at Fdef, deformation friction.

Deformation Friction and Viscoelasticity

Adhesive friction is the major contributor in tire traction, but it requires intimate contact between the two surfaces. Adhesive friction forces decrease drastically when the road surface is lubricated by dust, water, or ice. That's when deformation friction becomes more important.

Here's where another interesting property of rubber, viscoelasticity, comes into play. Rubber is elastic and conforms to surface irregularities. But rubber is also viscoelastic; it doesn't rebound fully after deformation. Press your thumbnail into a street tire and the rubber rebounds. Press it into a racing tire and the mark stays there, recovering only slowly. This is a simple but crude test of hysteresis, or energy loss, in rubber. Low-hysteresis rubber rebounds quickly; high-hysteresis rubber lags in rebound after deformation.

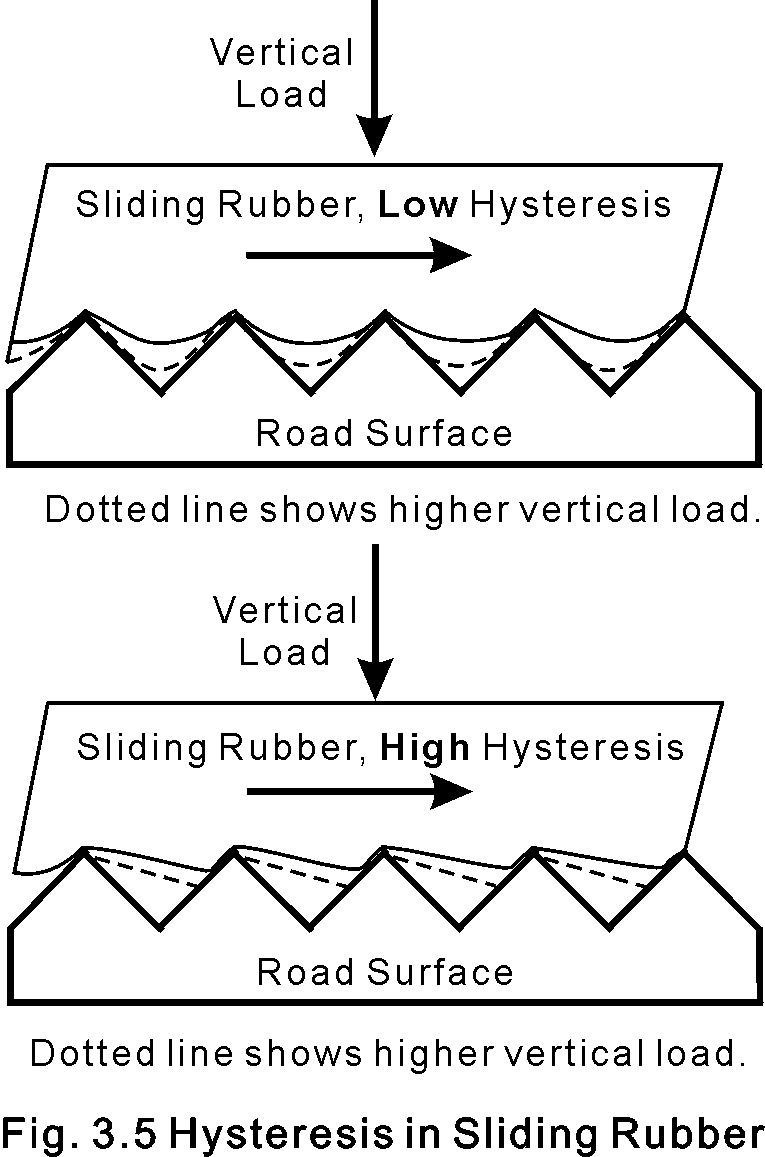
Consider Fig. 3.5 where there is some sliding between the rubber and an irregular surface. If the rubber recovers slowly from the passing irregularity as in the high-hysteresis rubber, it can't push on the downstream surfaces of the irregularities as hard as it pushes on the upstream surfaces. This pressure difference between the upstream and downstream faces of the irregularity results in friction forces even when the surfaces are lubricated.

An interesting analogy to rubber sliding past peaks in a road surface is a ship moving in water. We know a ship moving in water requires an engine and propeller to provide the necessary force to overcome fluid drag. The ship bumps into the still water at the bow and there is a little more pressure there than on the stern. It's this pressure difference acting over the wetted cross-sectional area of the ship's hull that is a part of the total drag the engines have to overcome. There is also viscous drag caused by the hull surface moving through the water.

Continuing with that same analogy, a ship traveling in "high-hysteresis water" would experience increased drag because the rubber would close in more slowly at the stern, creating a larger bow-to-stern pressure difference. In high-hysteresis rubber that's deformation friction. Fig. 3.5 depicts the concept of increasing pressure differences across asperities caused by high-hysteresis rubber.

A common test of hysteresis during rubber processing is called the rebound test. A rubber sample is formed into a flat, rectangular shape and attached to a wall. A steel ball on a string is anchored on the wall above the rubber sample. The ball is raised until the string is horizontal and taut. When released, the ball accelerates on the end of the string until it strikes the mounted sample. How far the ball rebounds is a measure of hysteresis. Short rebound is high hysteresis. If you're making a golf ball, you want the rubber to bounce the ball as far back as possible. If you're making tread rubber for race tires, you'd like the ball to splat against the wall with very little rebound.

Practical Examples of the Viscoelastic Properties of Rubber Friction

It turns out that both the adhesive and deformation components of rubber friction are highly viscoelastic, meaning the amount of friction force they generate is sensitive to the size of the aggregate in the road surface, the speed of penetration of the aggregate into the rubber, and the sliding speed of the rubber across that aggregate.
We know water is only slightly viscous, less so than motor oil or honey and certainly less than rubber. If you stick a finger into water you can hardly feel any resistance, only wetness. But if you slap the surface of a swimming pool you can hurt your hand. The water is viscous enough that it can't get out of the way if your hand is moving fast enough.

Here are two lightly edited excerpts from the book that illustrate how the viscoelasticity of rubber affects racers:

Road Surface Effects

After the 1996 season the racetrack at Laguna Seca near Monterey, Calif., was repaved. Testing by CART teams the next spring revealed much higher levels of grip and lap times dropped by seconds over previous events. But when the teams returned for their race at Laguna the following September, they found much lower grip levels and had to drastically change the setups they had so carefully developed six months earlier. During that race weekend I remember a couple of people attributing the problem to pavement wear, but didn't understand the phenomenon until I began to write these chapters.
Fresh pavement has sharp rocks sticking up through the asphalt matrix, and that's what the CART teams experienced at Laguna Seca immediately after the repaving. The high levels of grip made them all feel like heroes. But during the next six months the Russell Driving School cars and racecars competing in the many SCCA and vintage events polished off the sharp corners of the aggregate.

Wearing of the aggregate both lowers and rounds the peaks on the individual stones. It turns out that the shape and texture of road irregularities makes a difference.

The Myth of Off-Line in the Rain

We've probably all seen experienced drivers steer their cars off the normal line when cornering on wet pavement. The usual explanation is the normal line is slower in the wet because of oil and old rubber.

If there actually is more grip offline it's because the surface features are higher and more pointy than the more worn features on the normal line, providing higher deformation friction. This phenomenon is exaggerated by high-hysteresis compounds in racing rain tires. When dry the "line" is the fast way around that turn because it's shorter and has the biggest radius.

I've talked to several race drivers about this phenomenon and a couple of them pointed out that offline in the wet worked on dedicated racetracks and not on street courses. The reason for that is there is no "line" on a street course; the aggregate is worn everywhere by daily street traffic. But on a dedicated road course, 99% of the cars on the course are working the racing line and wearing the aggregate in the process. Off-line aggregate should be higher and more pointed.